981. Minimum spanning tree

Find the weight of minimum spanning tree for a weighted undirected connected graph.

Input. The first line contains the numbers n and m (1 ≤ n ≤ 100, 1 ≤ m ≤ 6000), where n is the number of vertices in the graph and m is the number of edges. Each of the next m lines contains a triple of integers a, b, c is written, where a and b are the numbers of vertices connected by an edge and c is the weight of edge (a positive number not exceeding 30000).

Output. Print the weight of minimum spanning tree.

Sample input	Sample output
3 3 1 2 1 2 3 2 3 1 3	3

SOLUTION

graphs – minimum spanning tree – Kruskal

Algorithm analysis

In this problem you must find the weight of the minimum spanning tree using Kruskal’s algorithm.

Example

The graph given in the sample has a form:

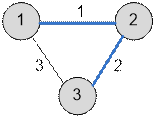
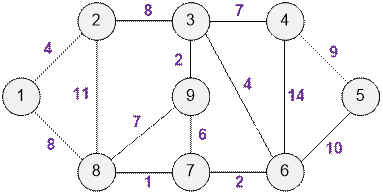
Exercise 1

Find the weight of the minimum spanning tree for the next graph.

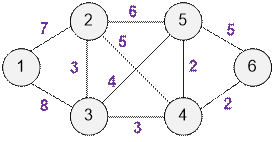
Exercise 2

Find the weight of the minimum spanning tree for the next graph.

Algorithm realization

Declare the structure of the graph edge (a pair of vertices and the weight of the edge). Declare the vector of edges e.

struct Edge

{

int u, v, dist;

};

vector<Edge> e;

Declare an array parent used by the disjoint set system.

vector<int> parent;

The function Repr finds a representative of the set that contains vertex n.

int Repr(int n)

{

while (n != parent[n]) n = parent[n];

return n;

}

Function Union unites sets that contain elements x and y.

int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return 0;

parent[y] = x;

return 1;

}

The function lt is a comparator for sorting edges.

int lt(Edge a, Edge b)

{

return (a.dist < b.dist);

}

The main part of the program. Initialize the parent array.

scanf("%d %d",&n,&m);

parent.resize(n + 1);

for (i = 1; i <= n; i++) parent[i] = i;

Read the edges of the graph.

e.resize(m);

for (i = 0; i < m; i++)

scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);

Sort the edges in increasing order of their weights.

sort(e.begin(), e.end(), lt);

Start the Kruskal algorithm that constructs the minimum spanning tree.

res = 0;

for(i = 0; i < m; i++)

if (Union(e[i].u,e[i].v)) res += e[i].dist;

Print the weight of the minimum spanning tree.

printf("%d\n",res);

Algorithm realization – heuristics

#include <cstdio>

#include <algorithm>

#include <vector>

using namespace std;

struct Edge

{

int u, v, dist;

};

vector<Edge> e;

vector<int> parent, depth;

int i, n, m, res;

int Repr(int n)

{

if (n == parent[n]) return n;

return parent[n] = Repr(parent[n]);

}

int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return 0;

if (depth[x] < depth[y]) swap(x, y);

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

return 1;

}

int lt(Edge a, Edge b)

{

return a.dist < b.dist;

}

int main(void)

{

scanf("%d %d", &n, &m);

parent.resize(n + 1);

depth.resize(n + 1);

for (i = 1; i <= n; i++)

{

parent[i] = i;

depth[i] = 0;

}

e.resize(m);

for (i = 0; i < m; i++)

scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);

sort(e.begin(), e.end(), lt);

res = 0;

for (i = 0; i < m; i++)

if (Union(e[i].u, e[i].v)) res += e[i].dist;

printf("%d\n", res);

return 0;

}

Algorithm realization – Prim

#include <cstdio>

#include <cstring>

#include <cmath>

#include <vector>

#include <algorithm>

#define MAX 101

#define INF 0x3F3F3F3F

using namespace std;

int i, n, m, a, b, c, res;

vector<vector<pair<int, int> > > g; // (to, dist)

int used[MAX], dist[MAX];

int Prim(int start)

{

memset(dist, 0x3F, sizeof(dist));

memset(used, 0, sizeof(used));

int i, j, cur = start, res = 0;

dist[cur] = 0;

used[cur] = 1;

for (i = 1; i < n; i++)

{

// cur -> to

for (j = 0; j < g[cur].size(); j++)

{

int to = g[cur][j].first;

int d = g[cur][j].second;

if (!used[to] && (d < dist[to]))

dist[to] = d;

}

int min = INF;

for (j = 1; j <= n; j++)

if (!used[j] && (dist[j] < min))

{

min = dist[j];

cur = j;

}

used[cur] = 1;

res += dist[cur];

}

return res;

}

int main(void)

{

scanf("%d %d", &n, &m);

g.resize(n + 1);

for (i = 0; i < m; i++)

{

scanf("%d %d %d", &a, &b, &c);

g[a].push_back(make_pair(b,c));

g[b].push_back(make_pair(a, c));

}

res = Prim(1);

printf("%d\n", res);

return 0;

}

Java realization

import java.util.*;

class Edge

{

int u, v, dist;

Edge (int u, int v, int dist)

{

this.u = u;

this.v = v;

this.dist = dist;

}

};

public class Main

{

static int mas[];

static int size[];

static int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

static int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if(x == y) return 0;

if (size[x] < size[y])

{

int temp = x; x = y; y = temp;

}

mas[y] = x;

size[x] += size[y];

return 1;

}

public static class MyFun implements Comparator<Edge>

{

public int compare(Edge a, Edge b)

{

return a.dist - b.dist;

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

mas = new int[n+1];

size = new int[n+1];

for(int i = 1; i <= n; i++)

{

mas[i] = i;

size[i] = 1;

}

Vector<Edge> v = new Vector<Edge>();

for(int i = 0; i < m; i++)

{

int x = con.nextInt();

int y = con.nextInt();

int dist = con.nextInt();

v.add(new Edge(x, y, dist));

}

Collections.sort(v, new MyFun());

int res = 0;

for(int i = 0; i < m; i++)

if (Union(v.get(i).u, v.get(i).v) == 1) res += v.get(i).dist;

System.out.println(res);

con.close();

}

}